Beregning av kabeltverrsnitt etter strøm og strøm: hvordan beregne ledninger riktig

Har du tenkt å gjøre modernisering av strømnettet eller i tillegg utvide strømledningen til kjøkkenet for å koble til en ny elektrisk komfyr? Her vil minimal kunnskap om lederens tverrsnitt og effekten av denne parameteren på effekt og strøm være nyttig.

Enig i at feil beregning av kabeltverrsnittet fører til overoppheting og kortslutning eller til uberettigede kostnader.

Det er veldig viktig å utføre beregninger på designstadiet, siden feil skjulte ledninger og etterfølgende utskifting er forbundet med betydelige kostnader. Vi vil hjelpe deg med å forstå vanskelighetene med beregninger for å unngå problemer med videre drift av elektriske nettverk.

For ikke å belaste deg med komplekse beregninger, har vi valgt klare formler og beregningsalternativer, presentert informasjonen i en tilgjengelig form og gitt formlene forklaringer. Tematiske bilder og videomateriale er også lagt til artikkelen, slik at du tydelig kan forstå essensen av problemet under vurdering.

Beregning av tverrsnitt for forbrukerkraft

Hovedformålet med ledere er å levere elektrisk energi til forbrukere i nødvendig mengde. Siden superledere ikke er tilgjengelige under normale driftsforhold, må motstanden til ledermaterialet tas i betraktning.

Beregning av nødvendig seksjon ledere og kabler avhengig av den totale kraften til forbrukerne er basert på langsiktig driftserfaring.

La oss begynne det generelle beregningsforløpet ved først å utføre beregninger ved å bruke formelen:

P = (P1+P2+..PN)*K*J,

Hvor:

• P – kraften til alle forbrukere koblet til den beregnede grenen i watt.
• P1, P2, PN – kraften til henholdsvis den første, andre, n'te forbrukeren i watt.

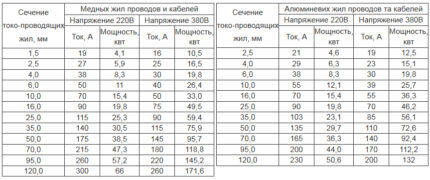
Etter å ha mottatt resultatet på slutten av beregningene ved hjelp av formelen ovenfor, var det på tide å gå til tabelldataene.

Nå må du velge ønsket seksjon i henhold til Tabell 1.

Tabell 1. Trådtverrsnittet skal alltid velges til nærmeste større side (+)

Trinn #1 - beregning av reaktiv og aktiv effekt

Forbrukerkapasitet er angitt i utstyrsdokumentene. Vanligvis indikerer utstyrsdatablad aktiv effekt sammen med reaktiv effekt.

Enheter med en aktiv type belastning konverterer all mottatt elektrisk energi, under hensyntagen til effektivitet, til nyttig arbeid: mekanisk, termisk eller annen type.

Enheter med aktiv belastning inkluderer glødelamper, varmeovner og elektriske komfyrer.

For slike enheter har beregningen av strøm etter strøm og spenning formen:

P=U*I,

Hvor:

• P – effekt i W;
• U – spenning i V;
• Jeg – strømstyrke i A.

Enheter med en reaktiv type belastning er i stand til å akkumulere energi som kommer fra en kilde og deretter returnere den. Denne utvekslingen skjer på grunn av forskyvningen av strømsinus og spenningssinus.

Ved null faseforskyvning har effekt P=U*I alltid en positiv verdi. Enheter med en aktiv type belastning har en slik graf over fasene til strøm og spenning (I, i - strøm, U, u - spenning, π - pi lik 3,14)

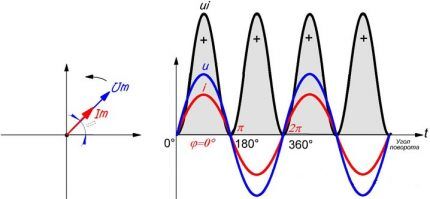
Enheter med reaktiv effekt inkluderer elektriske motorer, elektroniske enheter av alle størrelser og formål, og transformatorer.

Når det er en faseforskyvning mellom strømsinus og spenningssinus, kan effekten P=U*I være negativ (I, i - strøm, U, u - spenning, π - pi lik 3,14). En reaktiv kraftenhet returnerer lagret energi tilbake til kilden

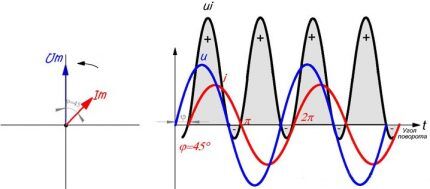
Elektriske nettverk er bygget på en slik måte at de kan overføre elektrisk energi i én retning fra kilde til last.

Derfor er den returnerte energien fra en forbruker med en reaktiv belastning parasittisk og går til spille på oppvarming av ledere og andre komponenter.

Reaktiv effekt avhenger av fasevinkelen mellom spennings- og strømsinusene. Faseforskyvningsvinkelen uttrykkes gjennom cosφ.

For å finne den totale kraften, bruk formelen:

P = Q / cosφ,

Hvor Q – reaktiv effekt i VAR.

Typisk indikerer enhetens datablad reaktiv effekt og cosφ.

Eksempel: passet til borhammeren indikerer en reaktiv effekt på 1200 VAr og cosφ = 0,7.Derfor vil det totale strømforbruket være lik:

P = 1200/0,7 = 1714 W

Hvis cosφ ikke ble funnet, kan cosφ for de aller fleste elektriske husholdningsapparater tas lik 0,7.

Trinn #2 - søk etter simultanitet og margin koeffisienter

K – dimensjonsløs simultanitetskoeffisient, viser hvor mange forbrukere som kan kobles til nettverket samtidig. Det skjer sjelden at alle enheter bruker strøm samtidig.

Samtidig drift av TV- og musikksenteret er usannsynlig. Fra etablert praksis kan K tas lik 0,8. Hvis du planlegger å bruke alle forbrukere samtidig, bør K settes til 1.

J – dimensjonsløs sikkerhetsfaktor. Karakteriserer opprettelsen av en kraftreserve for fremtidige forbrukere.

Fremgangen står ikke stille; hvert år oppfinnes nye fantastiske og nyttige elektriske enheter. Elektrisitetsforbruket forventes å vokse med 84 % innen 2050. Vanligvis er J antatt å være mellom 1,5 og 2,0.

Trinn #3 - utføre beregninger ved hjelp av den geometriske metoden

I alle elektriske beregninger tas lederens tverrsnittsareal - tverrsnittet av kjernen. Målt i mm².

Det er ofte nødvendig å lære å beregne riktig tråddiameter leder ledninger.

I dette tilfellet er det en enkel geometrisk formel for en monolittisk rund ledning:

S = π*R² = π*D²/4, eller vice versa

D = √(4*S / π)

For rektangulære ledere:

S = h * m,

Hvor:

• S – kjerneareal i mm²;
• R – kjerneradius i mm;
• D – kjernediameter i mm;
• h, m – henholdsvis bredde og høyde i mm;
• π — pi er lik 3,14.

Hvis du kjøper en trådet ledning, der en leder består av mange vridd ledninger med rundt tverrsnitt, utføres beregningen i henhold til formelen:

S = N*D²/1,27,

Hvor N – antall ledninger i kjernen.

Ledninger med kjerner vridd fra flere ledninger har generelt bedre ledningsevne enn monolittiske. Dette skyldes egenskapene til strømstrømmen gjennom en leder med rundt tverrsnitt.

Elektrisk strøm er bevegelsen av like ladninger langs en leder. Som ladninger frastøter hverandre, så blir ladningsfordelingstettheten forskjøvet mot overflaten av lederen.

En annen fordel med strandede ledninger er deres fleksibilitet og mekaniske motstand. Monolittiske ledninger er billigere og brukes hovedsakelig til stasjonær installasjon.

Trinn #4—beregn krafttverrsnittet i praksis

Oppgave: den totale effekten til forbrukere på kjøkkenet er 5000 W (som betyr at effekten til alle reaktive forbrukere er beregnet på nytt). Alle forbrukere er koblet til et enfaset 220 V-nettverk og får strøm fra én gren.

Tabell 2. Hvis du planlegger å koble til flere forbrukere i fremtiden, viser tabellen den nødvendige effekten til vanlige husholdningsapparater (+)

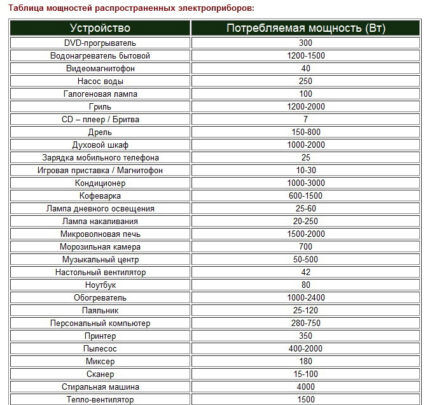
Løsning:

La oss ta samtidighetskoeffisienten K lik 0,8. Kjøkkenet er et sted for konstant innovasjon, man vet aldri, sikkerhetsfaktoren er J=2,0. Den totale estimerte effekten vil være:

P = 5000*0,8*2 = 8000 W = 8 kW

Ved å bruke verdien av den beregnede kraften ser vi etter den nærmeste verdien i tabell 1.

Det nærmeste egnede kjernetverrsnittet for et enfaset nettverk er en kobberleder med et tverrsnitt på 4 mm². Lignende ledningsstørrelse med 6 mm aluminiumskjerne².

For enkeltlederkabling vil minimumsdiameteren være henholdsvis 2,3 mm og 2,8 mm.Ved bruk av flerkjernealternativ summeres tverrsnittet til de enkelte kjernene.

Beregning av nåværende tverrsnitt

Beregninger av nødvendig strøm- og effekttverrsnitt av kabler og ledninger vil gi mer nøyaktige resultater.Slike beregninger gjør det mulig å evaluere den samlede påvirkningen av ulike faktorer på ledere, inkludert termisk belastning, merke av ledninger, type legging, driftsforhold, etc.

Hele beregningen utføres i følgende trinn:

• valg av makt for alle forbrukere;
• beregning av strømmer som går gjennom en leder;
• valg av passende tverrsnitt ved hjelp av tabeller.

For dette beregningsalternativet tas forbrukernes kraft i form av strøm og spenning uten å ta hensyn til korreksjonsfaktorer. De vil bli tatt i betraktning ved summering av strømstyrken.

Trinn #1 - beregning av strømstyrke ved hjelp av formler

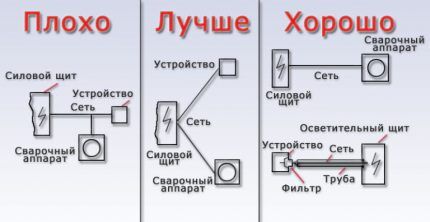
For de som har glemt skolefysikkkurset, tilbyr vi de grunnleggende formlene i form av et grafisk diagram som et visuelt jukseark:

"Classic Wheel" demonstrerer tydelig forholdet mellom formler og den gjensidige avhengigheten av egenskapene til elektrisk strøm (I - strømstyrke, P - effekt, U - spenning, R - kjerneradius)

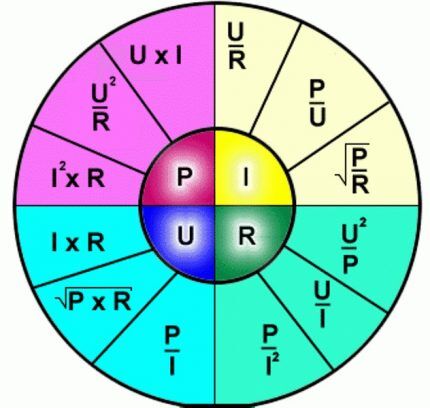
La oss skrive ned avhengigheten av strømmen I på kraften P og linjespenningen U:

I = P/U_l,

Hvor:

• Jeg — strømstyrke, tatt i ampere;
• P — effekt i watt;
• U_l — linjespenning i volt.

Nettspenningen avhenger generelt av strømforsyningskilden; den kan være en- eller trefaset.

Forholdet mellom lineær og fasespenning:

1. U_l = U*cosφ ved enfasespenning.
2. U_l = U*√3*cosφ ved trefasespenning.

For elektriske husholdningsforbrukere er cosφ=1 akseptert, så den lineære spenningen kan skrives om:

1. U_l = 220 V for enfasespenning.
2. U_l = 380 V for trefasespenning.

Deretter oppsummerer vi alle forbrukte strømmer ved å bruke formelen:

I = (I1+I2+…IN)*K*J,

Hvor:

• Jeg – total strøm i ampere;
• I1..IN – strømstyrken til hver forbruker i ampere;
• K – samtidighetskoeffisient;
• J - sikkerhetsfaktor.

Koeffisientene K og J har samme verdier som de som brukes ved beregning av totaleffekten.

Det kan være et tilfelle når det i et trefasenettverk strømmer en strøm med ulik styrke gjennom forskjellige faseledere.

Dette skjer når en-fase og tre-fase forbrukere er koblet til en tre-fase kabel samtidig. For eksempel drives en trefasemaskin og enfasebelysning.

Et naturlig spørsmål oppstår: hvordan beregnes tverrsnittet til en strandet ledning i slike tilfeller? Svaret er enkelt - beregninger er gjort basert på den mest belastede kjernen.

Trinn #2 - velge en passende seksjon ved hjelp av tabeller

Driftsreglene for elektriske installasjoner (PEU) inneholder en rekke tabeller for valg av nødvendig tverrsnitt av kabelkjernen.

Ledningsevnen til en leder avhenger av temperaturen. For metallledere øker motstanden med økende temperatur.

Når en viss terskel overskrides, blir prosessen selvopprettholdende: jo høyere motstand, jo høyere temperatur, jo høyere motstand osv. til lederen brenner ut eller forårsaker kortslutning.

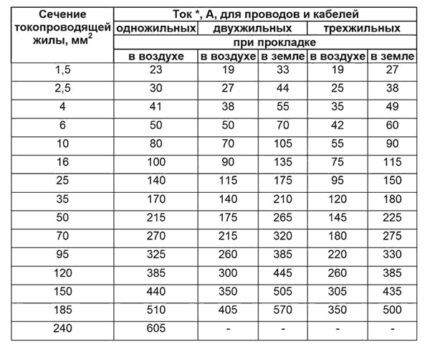
De neste to tabellene (3 og 4) viser tverrsnittet av ledere avhengig av strøm og installasjonsmetode.

Tabell 3. Først må du velge metode for å legge ledningene, dette bestemmer hvor effektiv kjølingen er (+)

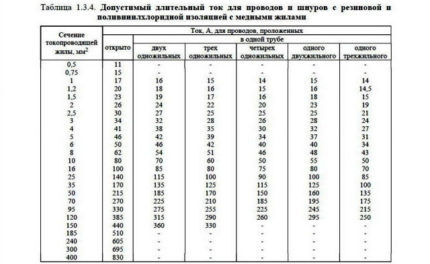
En kabel skiller seg fra en ledning ved at alle kabelkjerner, utstyrt med egen isolasjon, er tvunnet til en bunt og omsluttet i en felles isolasjonskappe. Flere detaljer om forskjellene og typene av kabelprodukter er skrevet i denne artikkel.

Tabell 4. Den åpne metoden er angitt for alle ledertverrsnittsverdier, men i praksis legges ikke seksjoner under 3 mm2 åpent på grunn av mekanisk styrke (+)

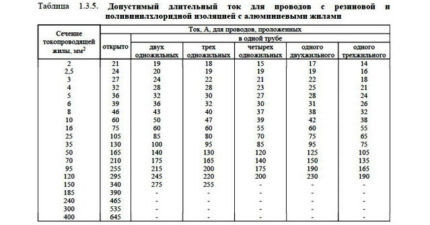
Ved bruk av tabeller brukes følgende koeffisienter på den tillatte kontinuerlige strømmen:

• 0,68 hvis 5-6 kjerner;
• 0,63 hvis 7-9 kjerner;
• 0,6 hvis 10-12 kjerner.

Reduksjonsfaktorer brukes på gjeldende verdier fra "åpne"-kolonnen.

Nøytral- og jordledere er ikke inkludert i antall ledere.

I henhold til PES-standarder er valget av tverrsnittet til nøytrallederen i henhold til den tillatte kontinuerlige strømmen gjort som minst 50% av faselederen.

De neste to tabellene (5 og 6) viser avhengigheten av den tillatte langtidsstrømmen når den legges i bakken.

Tabell 5. Avhengigheter av tillatt langtidsstrøm for kobberkabler når de legges i luft eller jord

Strømbelastningen når den legges åpent og når den legges dypt ned i bakken er forskjellig. De aksepteres som like dersom legging i bakken utføres ved bruk av brett.

Tabell 6. Avhengigheter av tillatt kontinuerlig strøm for aluminiumskabler når de legges i luft eller jord

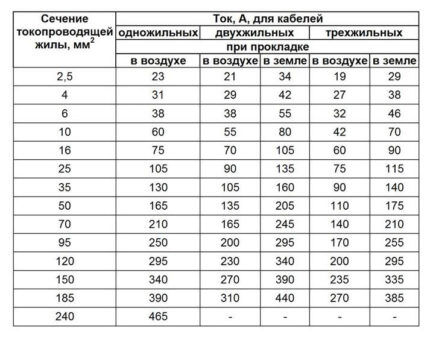
For installasjon av midlertidige strømforsyningsledninger (bærende, hvis for privat bruk), gjelder følgende tabell (7).

Tabell 7. Tillatt kontinuerlig strøm ved bruk av bærbare slangeledninger, bærbare slange- og akselkabler, flomlyskabler, fleksible bærbare ledninger. Kun kobberledere brukes

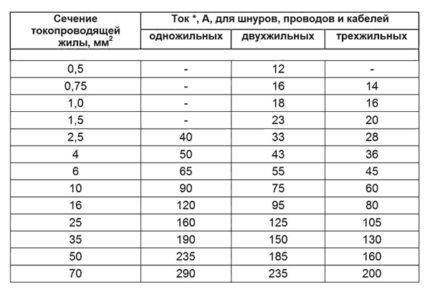
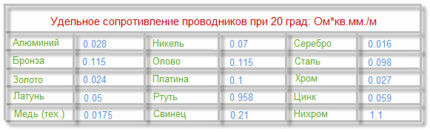
Ved legging av kabler i bakken, i tillegg til varmeavledningsegenskapene, er det nødvendig å ta hensyn til resistiviteten, som gjenspeiles i følgende tabell (8):

Tabell 8. Korreksjonsfaktor avhengig av jordtype og resistivitet for tillatt langtidsstrøm, ved beregning av kabeltverrsnitt (+)

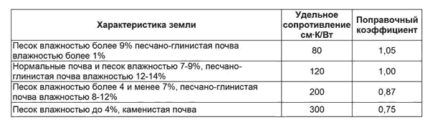
Beregning og valg av kobberkjerner inntil 6 mm² eller aluminium opptil 10 mm² utføres som for kontinuerlig strøm.

Ved store tverrsnitt er det mulig å bruke en reduksjonsfaktor:

0,875 * √T_pv

Hvor T_pv — forholdet mellom byttevarighet og syklusvarighet.

Varigheten av å slå på er antatt å være ikke mer enn 4 minutter. I dette tilfellet bør syklusen ikke overstige 10 minutter.

Ved valg av kabel for fordeling av strøm inn trehus Spesiell oppmerksomhet rettes mot brannmotstanden.

Trinn #3 - beregning av strømtverrsnittet til lederen ved hjelp av et eksempel

Oppgave: beregne den nødvendige delen kobberkabel for tilkobling:

• trefase trebearbeidingsmaskin med en effekt på 4000 W;
• trefase sveisemaskin med en effekt på 6000 W;
• husholdningsapparater i huset med en total effekt på 25 000 W;

Tilkoblingen vil bli laget med en femkjerners kabel (trefaseledere, en nøytral og en jording), lagt i bakken.

Isolasjonen til kabel- og ledningsprodukter beregnes for en bestemt driftsspenning. Det bør tas i betraktning at driftsspenningen til produktet hans angitt av produsenten må være høyere enn nettspenningen

Løsning.

Trinn 1. Vi beregner den lineære spenningen til en trefaseforbindelse:

U_l = 220 * √3 = 380 V

Steg 2. Husholdningsapparater, et maskinverktøy og en sveisemaskin har reaktiv effekt, så kraften til maskineriet og utstyret vil være:

P_de = 25000 / 0,7 = 35700 W

P_obor = 10000 / 0,7 = 14300 W

Trinn #3. Strøm som kreves for å koble til husholdningsapparater:

Jeg_de = 35700 / 220 = 162 A

Trinn #4. Strøm som kreves for å koble til utstyr:

Jeg_obor = 14300 / 380 = 38 A

Trinn #5. Den nødvendige strømmen for tilkobling av husholdningsapparater beregnes basert på en fase. I henhold til problemstillingen er det tre faser. Derfor kan strømmen fordeles mellom fasene. For enkelhets skyld antar vi en enhetlig fordeling:

Jeg_de = 162 / 3 = 54 A

Trinn #6. Strøm per fase:

Jeg_f = 38 + 54 = 92 A

Trinn #7. Utstyr og husholdningsapparater vil ikke fungere samtidig, i tillegg vil vi sette av en reserve på 1,5. Etter å ha brukt korreksjonsfaktorer:

Jeg_f = 92 * 1,5 * 0,8 = 110 A

Trinn #8. Selv om kabelen inneholder 5 kjerner, tas kun tre fasekjerner i betraktning. I følge tabell 8 i kolonnen trelederkabel i bakken finner vi at en strøm på 115 A tilsvarer et kjernetverrsnitt på 16 mm².

Trinn #9. I henhold til tabell 8 bruker vi en korreksjonsfaktor avhengig av karakteristikkene til landet. For en normal type jord er koeffisienten 1.

Trinn #10. Valgfritt, beregn diameteren til kjernen:

D = √(4*16 / 3,14) = 4,5 mm

Hvis beregningen bare ble gjort basert på kraft, uten å ta hensyn til særegenhetene ved kabellegging, ville tverrsnittet av kjernen være 25 mm². Å beregne strømstyrke er mer komplisert, men noen ganger kan du spare betydelige penger, spesielt når det gjelder flerkjernede strømkabler.

Du kan lese mer om forholdet mellom spennings- og strømverdier her.

Beregning av spenningsfall

Enhver leder, unntatt superledere, har motstand. Derfor, hvis kabelen eller ledningen er lang nok, oppstår det et spenningsfall.

PES-standarder krever at tverrsnittet av kabelkjernen er slik at spenningsfallet ikke er mer enn 5 %.

Tabell 9. Resistivitet til vanlige metallledere (+)

Dette gjelder først og fremst lavspentkabler med lite tverrsnitt.

Beregningen av spenningsfallet er som følger:

R = 2*(ρ * L) / S,

U_pad = I * R,

U_% = (U_pad /u_lin) * 100,

Hvor:

• 2 - koeffisient på grunn av det faktum at strømmen nødvendigvis flyter gjennom to ledninger;
• R – ledermotstand, Ohm;
• ρ — lederresistivitet, Ohm*mm²/m;
• S – ledertverrsnitt, mm²;
• U_pad – fall spenning, V;
• U_% - spenningsfall i forhold til U_lin,%.

Ved hjelp av formler kan du uavhengig utføre de nødvendige beregningene.

Bæreregneeksempel

Oppgave: beregn spenningsfallet for en kobbertråd med et tverrsnitt av en kjerne på 1,5 mm². Ledningen er nødvendig for å koble til en enfaset elektrisk sveisemaskin med en total effekt på 7 kW. Ledningslengde 20 m.

De som ønsker å koble en husholdningssveisemaskin til en elektrisk nettverksgren bør ta hensyn til strømsikten som kabelen som brukes er designet for. Det er mulig at den totale effekten til driftsenheter kan være høyere. Det beste alternativet er å koble forbrukere til separate filialer

Løsning:

Trinn 1. Vi beregner motstanden til kobbertråden ved å bruke tabell 9:

R = 2*(0,0175 * 20) / 1,5 = 0,47 Ohm

Steg 2. Strøm som flyter gjennom lederen:

I = 7000 / 220 = 31,8 A

Trinn #3. Spenningsfall på ledningen:

U_pad = 31,8 * 0,47 = 14,95 V

Trinn #4. Vi beregner prosentandelen av spenningsfallet:

U_% = (14,95 / 220) * 100 = 6,8%

Konklusjon: For å koble til sveisemaskinen kreves en leder med stort tverrsnitt.

Konklusjoner og nyttig video om temaet

Beregning av ledertverrsnittet ved hjelp av formlene:

Anbefalinger fra spesialister om valg av kabel- og ledningsprodukter:

Ovennevnte beregninger gjelder for kobber- og aluminiumsledere for industriell bruk. For andre typer ledere er den totale varmeoverføringen forhåndsberegnet.

Basert på disse dataene beregnes den maksimale strømmen som kan strømme gjennom lederen uten å forårsake overdreven oppvarming.

Hvis du har spørsmål om metoden for å beregne kabeltverrsnittet eller ønsker å dele din personlige erfaring, vennligst legg igjen kommentarer til denne artikkelen.Gjennomgangsdelen finner du nedenfor.