Ohms lov for en komplett kjede og for en del av en kjede: alternativer for å skrive formel, beskrivelse og forklaring

Det er ingen måte for en profesjonell elektriker eller elektronikkspesialist å omgå Ohms lov i sine egne aktiviteter, og løse eventuelle problemer knyttet til oppsett, justering og reparasjon av elektroniske og elektriske kretser.

Faktisk må alle forstå denne loven. For alle må forholde seg til strøm i hverdagen.

Og selv om den tyske fysikeren Ohms lov er fastsatt i ungdomsskolens læreplan, blir den i praksis ikke alltid studert i tide. Derfor vil vi i vårt materiale vurdere et så relevant emne for livet og forstå alternativene for å skrive formelen.

Enkeltseksjon og komplett elektrisk krets

Vurderer en elektrisk krets fra synspunktet om å anvende Ohms lov på en krets, bør to mulige beregningsalternativer bemerkes: for en egen seksjon og for en fullverdig krets.

Beregning av strømmen til en elektrisk kretsseksjon

En del av en elektrisk krets anses som regel å være den delen av kretsen som utelukker kilden til EMF, som har ekstra intern motstand.

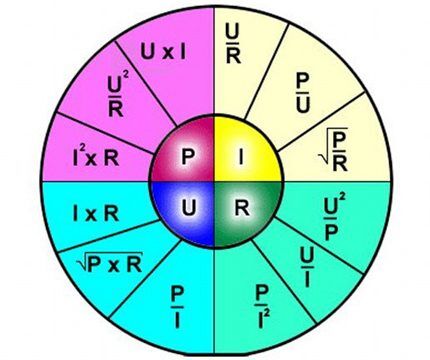
Derfor ser beregningsformelen, i dette tilfellet, enkel ut:

I = U/R,

Hvor henholdsvis:

• Jeg - strømstyrke;
• U – påført spenning;
• R - motstand.

Tolkningen av formelen er enkel - strømmen som strømmer gjennom en viss del av kretsen er proporsjonal med spenningen som påføres den, og motstanden er omvendt proporsjonal.

Den såkalte grafiske "daisy", der hele settet med varianter av formuleringer basert på Ohms lov presenteres. Praktisk verktøy for lommeoppbevaring: sektor "P" - kraftformler; sektor "U" - spenningsformler; sektor "I" - gjeldende formler; sektor "R" - motstandsformler

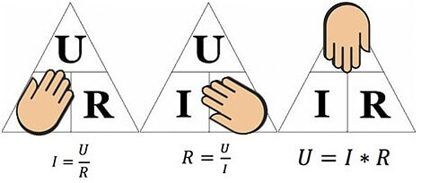
Således beskriver formelen tydelig avhengigheten av strømstrømmen gjennom en separat del av den elektriske kretsen i forhold til visse verdier av spenning og motstand.

Formelen er praktisk å bruke, for eksempel når du beregner parametrene til motstanden som må loddes inn i kretsen hvis spenningen og strømmen er gitt.

Ohms lov og to konsekvenser som enhver profesjonell elektromekanisk ingeniør, elektroingeniør, elektronikkingeniør og alle som er involvert i driften av elektriske kretser må vite. Fra venstre til høyre: 1 - gjeldende bestemmelse; 2 - bestemmelse av motstand; 3 - definisjon av spenning, hvor I - strøm, U - spenning, R - motstand

Figuren ovenfor vil bidra til å bestemme for eksempel strømmen som flyter gjennom en 10-ohm motstand som en spenning på 12 volt påføres. Ved å erstatte verdiene finner vi – I = 12 / 10 = 1,2 ampere.

Problemene med å finne motstand (når strømmen og spenningen er kjent) eller spenningen (når spenningen og strømmen er kjent) løses på lignende måte.

Dermed kan du alltid velge den nødvendige driftsspenningen, den nødvendige strømstyrken og det optimale resistive elementet.

Formelen som foreslås brukt krever ikke å ta hensyn til parametrene til spenningskilden.En krets som inneholder for eksempel et batteri, vil imidlertid bli beregnet ved hjelp av en annen formel. I diagrammet: A – slå på amperemeteret; V – slå på voltmeteret.

Forresten, tilkoblingsledningene til enhver krets er motstander. Mengden belastning de må bære bestemmes av spenningen.

Følgelig, igjen ved å bruke Ohms lov, blir det mulig å nøyaktig velge det nødvendige ledertverrsnittet, avhengig av kjernematerialet.

Vi har detaljerte instruksjoner på nettsiden vår kabeltverrsnittsberegning når det gjelder strøm og strøm.

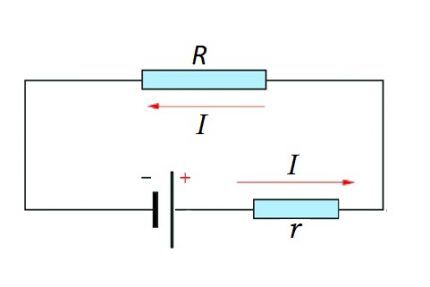
Beregningsmulighet for en komplett kjede

En komplett krets består av en seksjon (seksjoner), samt en kilde til EMF. Det vil si at den interne motstanden til EMF-kilden legges til den eksisterende resistive komponenten i kretsseksjonen.

Derfor er det logisk å endre formelen ovenfor litt:

I = U / (R + r)

Selvfølgelig kan verdien av den interne motstanden til EMF i Ohms lov for en komplett elektrisk krets betraktes som ubetydelig, selv om denne motstandsverdien i stor grad avhenger av strukturen til EMF-kilden.

Men når du beregner komplekse elektroniske kretser, elektriske kretser med mange ledere, er tilstedeværelsen av ytterligere motstand en viktig faktor.

For beregninger under forhold til en komplett elektrisk krets, tas alltid den resistive verdien til EMF-kilden i betraktning. Denne verdien summeres med den resistive motstanden til selve den elektriske kretsen. I diagrammet: I - strømflyt; R—eksternt resistivt element; r er den resistive faktoren til EMF (energikilden)

Både for en del av en krets og for en komplett krets bør det naturlige momentet tas i betraktning - bruken av konstant eller variabel strøm.

Hvis punktene nevnt ovenfor, karakteristiske for Ohms lov, ble vurdert fra synspunktet om å bruke likestrøm, ser alt derfor noe annerledes ut med vekselstrøm.

Hensyn til lovens effekt på en variabel mengde

Konseptet "motstand" mot betingelsene for å passere vekselstrøm bør betraktes mer som konseptet "impedans". Dette refererer til kombinasjonen av en resistiv belastning (Ra) og en reaktiv motstandsbelastning (Rr).

Slike fenomener er forårsaket av parametrene til induktive elementer og lovene for å bytte i forhold til en variabel spenningsverdi - en sinusformet strømverdi.

Dette er den ekvivalente kretsen til en elektrisk vekselstrømkrets for beregning ved bruk av formuleringer basert på prinsippene i Ohms lov: R - resistiv komponent; C er den kapasitive komponenten; L—induktiv komponent; EMF er en energikilde; I - strømflyt

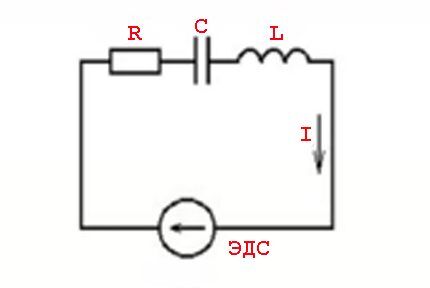
Med andre ord er det en effekt av strømverdier som leder (etterslep) fra spenningsverdier, som er ledsaget av utseendet til aktive (resistive) og reaktive (induktive eller kapasitive) krefter.

Slike fenomener beregnes ved hjelp av formelen:

Z=U/I eller Z = R + J * (X_L -X_C)

Hvor: Z - impedans; R - aktiv belastning; X_L , X_C – induktiv og kapasitiv belastning; J - koeffisient.

Seriell og parallell kobling av elementer

For elementer i en elektrisk krets (seksjon av en krets) er et karakteristisk punkt en seriell eller parallell forbindelse.

Følgelig er hver type tilkobling ledsaget av et annet mønster av strømflyt og spenningsforsyning.I denne forbindelse brukes Ohms lov også annerledes, avhengig av muligheten for å inkludere elementer.

Krets av seriekoblede resistive elementer

I forhold til en seriekobling (en del av en krets med to komponenter), brukes følgende formulering:

• jeg = jeg₁ = jeg₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Denne formuleringen viser tydelig at uavhengig av antall resistive komponenter koblet i serie, endres ikke strømmen som flyter gjennom en del av kretsen i verdi.

Kobling av resistive elementer i en del av kretsen i serie med hverandre. Dette alternativet har sin egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U, U1, U2 - påført spenning

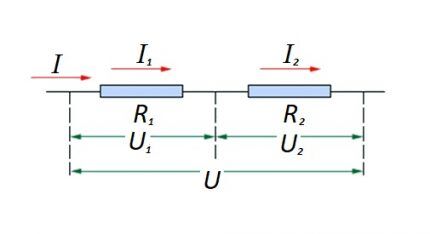
Størrelsen på spenningen som påføres de effektive resistive komponentene i kretsen er summen og summerer verdien av emk-kilden.

I dette tilfellet er spenningen på hver enkelt komponent lik: Ux = I * Rx.

Den totale motstanden bør betraktes som summen av verdiene til alle resistive komponenter i kretsen.

Krets av parallellkoblede resistive elementer

I tilfellet når det er en parallell forbindelse av resistive komponenter, anses følgende formulering som rettferdig i forhold til loven til den tyske fysikeren Ohm:

• jeg = jeg₁ +I₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Alternativer for å lage kretsseksjoner av "blandet" type, når parallelle og serielle forbindelser brukes, er ikke utelukket.

Kobling av resistive elementer på en del av en krets parallelt med hverandre. For dette alternativet brukes en annen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U er den tilførte spenningen; A, B - inn-/utgangspunkter

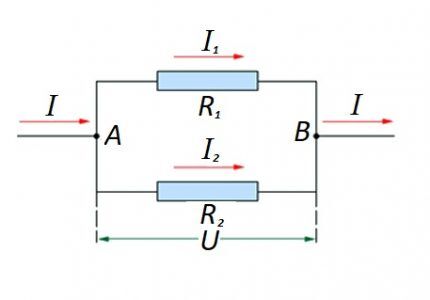
For slike alternativer utføres beregningen vanligvis ved først å beregne motstandsvurderingen til parallellforbindelsen. Deretter legges verdien til motstanden koblet i serie til det oppnådde resultatet.

Integrerte og differensielle former for loven

Alle punktene ovenfor med beregninger gjelder forhold når ledere av så å si "homogen" struktur brukes i elektriske kretser.

I mellomtiden må man i praksis ofte forholde seg til konstruksjonen av skjemaer, hvor strukturen til lederne endres i forskjellige seksjoner. For eksempel brukes ledninger med et større tverrsnitt eller omvendt en mindre, laget av forskjellige materialer.

For å ta hensyn til slike forskjeller, er det en variant av den såkalte "differensial-integral Ohms lov." For en infinitesimal leder beregnes strømtetthetsnivået avhengig av spennings- og konduktivitetsverdien.

Følgende formel brukes for differensialberegning: J = ό * E

For integralberegningen er derfor formuleringen: I * R = φ1 – φ2 + έ

Imidlertid er disse eksemplene ganske nærmere skolen for høyere matematikk og brukes faktisk ikke i den virkelige praksisen til en enkel elektriker.

Konklusjoner og nyttig video om temaet

En detaljert analyse av Ohms lov i videoen nedenfor vil bidra til å endelig konsolidere kunnskap i denne retningen.

En unik videoleksjon forsterker kvalitativt den teoretiske skriftlige presentasjonen:

Arbeidet til en elektriker eller aktiviteten til en elektronikkingeniør er integrert forbundet med øyeblikk hvor man faktisk må overholde Georg Ohms lov i aksjon. Dette er en slags truismer som enhver profesjonell bør vite.

Omfattende kunnskap om dette problemet er ikke nødvendig - det er nok å lære de tre hovedvariasjonene av ordlyden for å kunne bruke den i praksis.

Vil du supplere materialet ovenfor med verdifulle kommentarer eller si din mening? Skriv kommentarer i blokken under artikkelen. Hvis du har spørsmål, ikke nøl med å spørre våre eksperter.